Emilie och Emmy

Emilie du Chatelet (1706 - 1749) fick av sin far samma utbildning som hennes bröder, bl.a fäktning, ridning och gymnastik. Vid tolv års ålder talade hon latin, italienska, grekiska och tyska, samt givetvis sitt modersmål franska. Hon fick däremot inte någon tidig utbildning i matematik eller metafysik.
Hon tillhörde dock överklassen vilket gav henne rätt stora friheter. Efter att ha fött tre barn så flyttade hon och hennes man isär och började att ha älskare istället, vilket var accepterat i hennes kretsar. Av dessa så uppmuntrade duc de Richelieu henne att ånyo utforska matematiken. Hennes lärare blev 1733 Maupertuis. Hon kom sen att bli vän för livet med Voltaire.
Kring 1738 publicerade Kungliga Vetenskapsakademin en dissertation av henne om eld. Det var det första som de gav ut av en kvinna. Hon beskriver bl.a vad som senare kom att kallas infraröd strålning.
Hennes ”Lektioner i fysik” gavs ut 1740. Hon förklarar där Descartes, Leibniz och Newtons upptäckter. Hon kombinerar även teori med praktiska observationer av en Gravesande och kan korrigera Newton och andra med att säga att energin för ett objekt i rörelse är proportionellt till dess massa och *kvadraten* av dess hastighet (E ~ mv²).
Hon skrev även om religion och var lingvist och musiker. I Discours sur de bonheur som publicerades samma år som hon dog så skriver hon om sina passioner för studier, vetgirighet, spel och sex. Hon dog vid 42 års ålder i komplikationer efter en förlossning.
Samma år som hon dog så slutförde hon översättningen av Newtons Principia till franska, med hennes kommentar som innehöll hennes slutsats om idén ”energins bevarande”, vilken hon drog utifrån Newtons mekaniska principer. Den publicerades först tio år efter hennes död. Hennes översättning används fortfarande i Frankrike. Principen om energins bevarande skulle senare utvecklas vidare av Noether.
Om det ligger nånting i reinkarnation så gissar jag att du Chatelet återföddes som Amalie Emmy Noether (1882 - 1935), mest känd för Noethers sats, som säger att varje kontinuerlig symmetri inom fysiken svarar mot en bevarandelag.
Emmy Noether var dotter till en matematiker men kvinnor var vid denna tid utestängda från högre matematiska studier i Tyskland. Noether utbildade sej först till språklärare i engelska och franska men utbildade sej sedan inofficiellt inom matematik. Hon fick närvara vid föreläsningar om föreläsarna gav sitt tillstånd.
Hon var en optimistisk och social person, uppslukad av matematiska problem och brydde sej inte mer om sitt uteende än vad männen gjorde om sitt.
Hon lyckades doktorera med en avhandling om invariatanalys men fick inte hålla den föreläsning som var obligatorisk. Albert Einstein drog nytta av hennes resultat inom invariatanalysen och prisade henne i ett brev till matematiken David Hilbert. Med Hilberts hjälp så blev Noether 1919 privatdocent utan lön.
Invariatanalysen ledde till Noethers sats. Annars så sysslade hon inte så mycket med fysik.
Den allmänna relativitetsteorin som publicerades 1915 hade vissa problem med energins bevarande. Trots att ett flertal lärda professorer jobbade med problemet så var det Noether som löste det.
Det finns i fysiken ett flertal konserveringslagar som t.ex lagen om energins bevarande, lagen om rörelsemängdens bevarande och lagen om bevarande av elektrisk laddning.
Dessa lagar beskriver vad som inte förändras efter en viss händelse.
Noethers sats anknyter varje konserveringslag till en underliggande fysisk symmetri.
Detta var ett nytt och på sätt och vis genialiskt enkelt sätt att se på saken.
Empiriska iaktagelser förvandlas till begreppsliga självklarheter.
Efter denna utflykt till fysiken så återvände hon till den rena matematiken. Noether kom på att man borde studera de processer som bevarar matematiska strukturer. Efter 1919 jobbade hon med idealteori inom abstrakt algebra.
”Abstract algebra can be dated from the publication of two papers by Noether,”
-Nathan Jacobson
Hon publicerade sällan i eget namn. Hon samarbetade ofta med andra. Hon förelog ofta idéer som senare publicerades av hennes elever. Elever sökte sej till henne långväga ifrån.
Noether brukade inte skriva formler på svarta tavlan under tystnad utan diskuterade matematiska idéer med sina elever som om det vore en sorts filosofi.
"She taught us to think in simple, and thus general, terms... and not in complicated algebraic calculations,"
- P.S. Alexandroff
Efter 1927 jobbade hon med ickekommutativ algebra m.m.
”The theory of non-commutative algebras and their representations was built up by Emmy Noether in a new unified, purely conceptual manner by making use of all the results that has been accumulated by the ingenious labors of decades”
-Hermann Weyl
Hon sägs ha varit en av inspirationskällorna till kategoriteori. Saunders Mac Lane som grundade kategoriteorin tillsammans med Samuel Eilenberg hade studerat under Noether. Lawveres och Schanuels introduktionsbok i kategoriteori heter ”Conceptual math”
Det var inte bara som kvinna som hon avvek från normen. I sin ungdom var hon socialist och pacifist men när hon blev äldre så diskuterade hon sällan politik. 1933 tvingades hon som judinna fly till USA där hon fick en gästprofessur. Bara två år senare så avled hon efter en livmodersoperation, 53 år gammal.
Både Emilie och Emmy älskade att dansa.

Absolut negativ temperatur
I Kina finns exempel på att man räknade med negativa tal redan under antiken. För det mesta så har dock matematiker under historien varit negativa när de har snubblat över idén med negativa tal.
Via Indien och muslimska världen så nådde idén fram till Europa där t.ex Fibonacci (1170-1250) accepterade negativa tal åtminstone inom ekonomin, där de kunde tolkas som skuld. De flesta kallade dock negativa tal för absurda.
När Leibniz uppfann den matematiska analysen så blev dock negativa tal en nödvändighet och folk började att acceptera dem.
John Wallis konstaterade 1656 att 1/a krympte mot noll när a växte mot oändligheten och att 1/oändligt blev noll. När a krympte mot noll så växte kvoten mot oändligheten. Ett delat med ett negativt tal borde därför bli större än oändligheten.
Euler kom fram till samma slutsats 1746. Både Wallis och Euler missförstods som att de menade att alla negativa tal var större än oändligheten.
Wallis hade faktiskt också uppfunnit tallinjen där alla positiva tal står skivna på ett streck, och han hade även dragit ut strecket åt andra hållet och skrivit de negativa talen där, på andra sidan om nollan. Tallinjen började tydligen inte användas i vanlig undervisning förrän efter andra världskriget.
1956 kom ett av de första vetenskapliga arbeterna om negativa absoluta temperaturer inom fysiken. Detta har alltså ingenting att göra med de negativa temperaturer som vi talar om till vardags.
Om man har ett system, som en partikel eller flera, som har en negativ temperatur, och det systemet kommer i kontakt med ett annat system med positiv temperatur, så kommer energi att flöda från systemet med negativ temperatur till systemet med positiv temperatur, oavsett hur varmt systemet med positiv temperatur än är.
Eftersom energi flödar från varmare system till kallare system så kan man alltså säga att negativa temperaturer är varmare än någon positiv temperatur, eller ”mer än oändligt varmt”.
Detta fungerar bara om man har en övre gräns för hur mycket energi ett system kan ha. Detta hittar man egentligen bara inom kvantfysiken. I klassisk fysik så finns inget liknande.
Teoretiskt så använder man sej av en temperaturskala som är en cirkel. Ena halvan är positiva temperaturer och andra halvan är negativa temperaturer. Bägge sidorna går från noll till oändligheten. Här blir verkligen alla de negativa talen större än oändligt liksom de även är mindre än noll, samtidigt. Den kommer inte från Wallis, Leibniz eller Euler, så jag undrar var den kommer ifrån?
Herr Warum
There would be no danger of an atomic war if advances in history, the science of right and of state, philosophy, psychology, literature, art, etc. were as great as in physics. But instead of such progress, one is struck by significant regresses in many of the spiritual sciences.
-Gödel
Kurt Gödel föddes 1906 i Österike-Ungern. När han var tolv splittrades landet och han föll till den tjeckoslovakiska sidan. När han var 23 valde han att bli österrikare istället. När han var 32 annekterade Tyskland Österike och Gödel blev nu tysk. När han var 42 blev han amerikansk medborgare, vilket han var till sin död 71 år gammal.
Som tonåring läste han bl.a Göthe, Newton och Kant. Han tänkte först bli fysiker men läste ocskå matematik och filosofi. Han deltog i Wienkretsens möten med bl.a Carnap. 1928 var han på ett seminarium där frågan ställdes:
”Are the axioms of a formal system sufficient to derive every statement that is true in all models of the system?”
Det blev ämnet för hans doktorsavhandling som han färdigställde året efter. I den la han fram sitt ”Fullständighetsteorem”. Året efter, 1930, så blev han doktor. 1931 la han så fram sitt ”Ofullständighetsteorem”, vid 25 års ålder.
”I was a conceptual and mathematical realist since about 1925. I have never held the view that mathematics is syntax of language. Rather this view, understood in any reasonable sense, can be disproved by my results.”
-Gödel
Han visar där att ett matematiskt system inte samtidigt kan vara både fullständigt och motsägelsefritt. Innan hade alla antagit att ett matematiskt system självklart kunde vara både fullständigt och motsägelsefritt samtidigt och många hade försökt att skapa ett sånt system.
För detta har han kallats 1900-talets störste logiker och andra har sagt att detta var det viktigaste framsteget i logik sen Aristoteles.
(Iofs så hände just ingenting inom logiken efter Aristoteles på kanske tusen år.)
Gödels egen filosofiska tolkning av detta tycks ha varit att matematiken existerar oberoende av oss och vad vi kan veta och bevisa, tvärtom mot vad t.ex Carnap trodde.
1933 tog nazisterna makten i Tyskland. Gödel själv var tysktalande protestant men många av hans vänner och arbetskamrater var judar. Samma år besökte Gödel USA för första gången och träffade bl.a Einstein. Med åren skulle de bli bästa vänner.
1936 mördades hans vän logikern Moritz Schlick. Efter detta började Gödel att visa tecken på paranoia som till och från skulle följa honom resten av livet.
Gödel gifte sej 1938. Samma år tog Nazityskland över Österrike. Som känd judevän tyckte den nya regimen att Gödel skulle passa bättre som soldat än vid något universitet. Så 1939-40 så flydde Gödel och hans fru till USA där han senare blev medborgare. Resan tog ett tag eftersom de inte tog vägen över Atlanten utan reste åt andra hållet, runt Jorden. Så de fick en lång bröllopsresa.
Redan 1940 kunde han ge ut sitt arbete om kontinuumhypotesen och ”axiom of choice”. Även detta anses vara ett mycket viktigt och inflytelserikt arbete.
1947 följde Einstein och en annan vän honom till hans medborgarskapsintervju. Allt gick bra tills domaren som förhörde Gödel frågade om han trodde att en diktatur som den i Tyskland skulle kunna utvecklas i USA. Gödel började då förklara en brist han hade upptäckt i USAs konstitution som gjorde att detta kunde hända. Domaren var dock en vän till Einstein och hade bestämt sej för att godkänna Gödel så han avbröt denne innan han hann göra bort sej.
Att Gödel med största säkerhet liksom alla europeriska intellektuella var övervakad kunde säkert inte ha varit bra för hans paranoia. Hemingway tog sitt liv för att han kände sej förföljd och trodde att han höll på att bli galen. Senare visade det sej att de mycket riktigt övervakade honom.
Efter 40-talet så publicerade Gödel aldrig något mer officiellt, men han fortsatte att arbeta. Med åren så gled hans intresse tillbaka till fysik och filosofi, som han hade varit intresserad av i sin ungdom.
1949 presenterade Gödel en modell av ett universum som han hade skapat utifrån Einsteins teorier och ekvationer. Gödels lösning innebar ett roterande universum som inte utvidgade sej men där det var möjligt att tiden skulle kunna skapa en sluten cirkel så att framtiden till sist satt ihop med det förflutna. Detta universum tycks vara teoretiskt fullt möjligt men verkar inte stämma in på iaktagelserna av vårt eget universum. Gödel själv tycks dock ha frågat folk ibland om forskarna ännu trodde att universum roterade. Stephen Hawking verkar anse att Gödels modell skulle kunna utvecklas så att det skulle kunna passa in på vårt universum.
Economist Oskar Morgenstern recounts that toward the end of his life Einstein confided that his "own work no longer meant much, that he came to the Institute merely ... to have the privilege of walking home with Gödel”.
-Wikipedia
Efter Wittgensteins död 1951 publicerades bl.a en bok där han bl.a diskuterar Gödels ofullständighetsteorem och efter Gödels död har man bland hans opublicerade material hittat kommentarer om att Wittgenstein har missförstått honom fullständigt och Gödel undrar även om det kan vara avsiktligt.
Mellan 1943 och 1958 försökte Gödel att utarbeta en matematikfilosofi som dessutom skulle vara ett förarbete till en metafysik. Vid 1958 tyckte Gödel sej ha bevisat att Carnaps uppfattning om matematiken som en generell språksyntax var felaktig men han tyckte sej inte ha presterat något tillräckligt bra alternativ. Så Gödel började 1959 att läsa Husserl och var speciellt intresserad av hans ”kategoriska intuition”.
1928 skrev Husserl att “The ideal of the future is essentially that of phenomenologically based (“philosophical”) sciences, in unitary relation to an absolute theory of monads”. Husserl nämner några gånger idén om en ”fenomenologisk monadologi”. Gödel verkar vilja använda Husserl och Leibniz för att utveckla en filosofisk grund för matematiken och alla vetenskaper.
Ungefär 1960 skrev Gödel ner sin filosofi i 14 korta punkter:
”1. The world is rational.
2. Human reason can, in principle, be developed more highly (through certain techniques).
3. There are systematic methods for the solution of all problems (also art, etc.).
4. There are other worlds and rational beings of a different and higher kind.
5. The world in which we live is not the only one in which we shall live or have lived.
6. There is incomparably more knowable a priori than is currently known.
7. The development of human thought since the Renaissance is thoroughly intelligible (durchaus einsichtige).
8. Reason in mankind will be developed in every direction.
9. Formal rights comprise a real science.
10. Materialism is false.
11. The higher beings are connected to the others by analogy, not by composition.
12. Concepts have an objective existence.
13. There is a scientific (exact) philosophy and theology, which deals with concepts of the highest abstractness; and this is also most highly fruitful for science.
14. Religions are, for the most part, bad-- but religion is not.”
1970 avslöjade Gödel sitt gudsbevis som han hade skapat redan 1941 och sedan hållit hemligt tills han nu trodde at han var döende. Det var en variant av det ontologiska gudsbeviset, som allra först hade skapats av Anselm av Canterbury och som sedan hade utvecklats av Leibniz. Gödel försöker att formulera detta i samtida modallogik. Detta har bl.a lett till att dataforskare har intresserat sej för problemet.
”My belief is theistic, not pantheistic, following Leibniz rather than Spinoza.”
-Gödel
Mot slutet av sitt liv blev Gödel god vän med Hao Wang och denne släppte efter Gödels död boken ”A logical journey: From Gödel to philosophy”, där han beskriver Gödels filosfiska utveckling.
”The last time I spoke with Kurt Gödel was on the telephone, in March 1977. I had been studying the problem of whether machines can think, and I had become interested in the distinction between a system’s behavior and the underlying mind or consciousness, if any.
… I had begun to think that consciousness is really nothing more than simple existence. By way of leading up to this, I asked Gödel if he believed there is a single Mind behind all the various appearances and activities of the world.
He replied that, yes, the Mind is the thing that is structured, but that the Mind exists independently of its individual properties.
I then asked if he believed that the Mind is everywhere, as opposed to being localized in the brains of people.
Gödel replied, “Of course. This is the basic mystic teaching.”
-Rudy Rucker’s Infinity and the Mind,

Kommer vi att kunna använda det här i verkligheten, majjen?
I was a conceptual and mathematical realist since about 1925. I have never held the view that mathematics is syntax of language. Rather this view, understood in any reasonable sense, can be disproved by my results.
-Gödel
Jag brukar ofta försöka att vara pedagogisk på den här bloggen. Några av de pedagogiska principer som jag försöker att följa är att konkretisera det abstrakta, personifiera det opersonliga, att skapa relationer till det ointressanta och att göra historier av det kaotiska.
Vår hjärna är byggd för att hantera konkreta saker. Det är lättare att hantera det abstrakta om vi väljer att tolka det som konkret.
Det går alltid att hitta konkreta exempel på all matematik som man vill lära ut. En god lärare klarar också av detta.
Att lösa ett problem i taget är att tänka konkret. Att lösa flera problem på en gång är att tänka abstrakt.
Detta leder bl.a till att det finns ingen tydligt skiljelinje mellan ren och tillämpad matematik.
Jag har delvis svårt att ta till mej matematikundervisning eftersom de nybörjartexter som jag hittar är formalistiska medan jag är en matematisk realist. Jag skulle föredra om matematisk formalism kallades för matematisk skepticism eller matematisk nihilism.
Realism betyder bl.a att matematiska fenomen är aldrig identiska med sina definitioner, som så ofta hävdas. Man bör alltid räkna med att det finns något okänt hos varje matematiskt fenomen.
Matematiska objekt visar sina olika sidor och egenskaper när de sätts i olika sammanhang, inte när de isoleras maximalt.
Istället för att ge olika konkreta exempel på en matematisk princip för att visa hur den dyker upp i olika sammanhang så ges man en abstrakt regel att nöta in utantill därför att det finns ingenting att ”förstå”. Detta visar åtminstone att såna lärare öppet påstår sej inte ha förstått nånting.
Oavsett om formalismen är sann eller inte så mynnar den åtminstone i dålig pedagogik.
Inte ens de grundläggande siffrorna vet vi allt om. ”Ett” och ”noll” är väl så enkelt och utforskat som det kan bli? Matematikerna har dock nyligen upptäckt att ett inte är ett primtal och att noll är ett jämt tal.
Kurt Gödel var matematisk platonist, WVO Quine var matematisk empirist och Anders Tegmark är en matematisk monist. Alla dessa räknas som varianter av matematisk realism. Quine har jag tidigare skrivit om och Gödel kommer det snart mer om.
Anders Tegmark anser ju att alla matematiska former har fysisk existens, men i olika universum eftersom de inte kan existera i samma fysiska universum samtidigt. Så för honom så är matematiken en grund för fysiken. Nu så delar jag inte exakt hans teori men han är ändå en relativt känd fysiker som anser att matematiken är reell och att detta är viktigt för fysiken och kosmologin.
Matematiken är för mej en objektiv verklighet. Logicism/konstruktivism/formalism o.dyl. funkar dåligt för mej. Den gör matematiken helt platt och livlös. Per definition meningslös. Egentligen så skulle det inte kunna finnas något okänt i matematiken att forska i om konstruktivismen eller logicismen vore sann. Om hela matematiken vore en enda stor tautologi så vore den helt ointressant och helt oanvändbar. Att göra matematiken till en stor tautologi är idag möjligen ett framtida mål, inte ett faktum.
Logicismen nämns ibland som ett alternativ. Den skapades urspungligen av Frege och innebär att matematiken är härledbar från formell logik. Frege själv tycks ha haft en filosofiskt "realistisk" syn på logiken. Den ursprungliga logicismen är motbevisad men det finns neo-logicister eller neo-Fregenister som vill förespråka och förnya projektet även idag.
Formalism är närbesläktat med matematisk fiktionalism, konventionalism, psykologism, intuitionism och konstruktivism. Det finns även sociologer som hävdar att matematiken är en skapelse av samhället och marxister som anser att matematiken har förvridits av klassamhället. Dessa kan vara inspirerade av t.ex Wittgenstein eller Durkheim.
Den bortre frontlinjen inom teortisk fysik skulle kunna vara sökandet efter m-teorin och man har sett intressanta överrensstämmelser med ett esoteriskt område inom den avancerade matematiken: ett matematiskt objekt som kallas E11. Eftersom bägge dessa områden är mycket svårutforskade så går utvecklingen långsamt men det låter mycket intressant.
M-teorin är ju en förmodad teori som förenar alla de olika strängteorierna. I strängteorierna är allt vibrerande strängar och olika partiklar får sina olika egenskaper främst från hur strängarna vibrerar.
Inom algebra så kan bara det komplexa planet med komplexa tal användas för att lösa alla algebraiska ekvationer, inte naturliga tal eller nått sånt. Det komplexa planet skulle kunna tolkas som att objekt bara är specialfall av vågor.
Fourieranalys är en av de mest användna teknikerna och den beskriver vibrationer. Så verkligheten verkar i hög grad beröra oss som vibrationer.
Så på flera olika sätt så verkar matematisk forskning vilja antyda att vibrationer är något grundläggande för vår omvärldsförståelse.
En annan intressant idé är att relatera matematikens filosofi till filosofins matematik, som jag har skrivit något litet om här.
Erlangenprogrammet
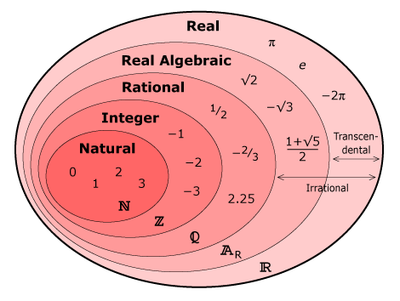
Jag har tidigare skrivit om hur olika talmängder förhåller sig till varandra; att man kan tala om en hierarki från de naturliga talen till de transcendentala talen.
Man kan även göra en liknande sak inom geometrin.
Förutom talteorin så är geometrin den kanske äldsta grenen av matematiken.
De finns idag en mångfald av olika geometrier och man kan även sätta vissa av dessa i en hierarki till varandra.
Under 1800-talet fann man sej för första gången i historien med en mångfald av geometrier.
Felix Klein och hans Erlangenprogram löste hur man skulle relatera dem till varandra.
Alla dessa nya geometrier kunde väl inte vara lika "sanna" som den klassiska euklidiska geometrin?
Jodå, svarade Klein.
Erlangenprogrammet såg euklidisk och ickeeuklidisk geometri som två sidor av samma sak.
På sin tid var det revolutionerande men idag så är det självklart.
Att öht ha olika "geometrier" som man försökte att relatera till varandra innebar en ny epok inom matematiken.
Olika geometrier betraktas av Klein som grupper, enligt "gruppteorin", som vara ganska ny då.
Projective>Affine>Similarity>Euclidian
Affin geometri hamnar mellan projektiv geometri och euklidisk geometri på så sätt att den åenasidan är identisk med euklidisk geometri utan kongruens, och åandrasidan är identisk med projektiv geometri om ett partikulärt plan eller linje får representera punkterna vid oändligheten.
1912 så utvecklade Wilson och Lewis en affin geometri för att uttrycka den speciella relativitetsteorin.
Den mest generella geometrin med minst antal lagar eller begränsningar är den projektiva.
De övriga geometrierna får man genom att lägga till ytterliggare lagar till den projektiva geometrin.
Detta gör att de övriga geometrierna kan liknas vid objekt inom den projektiva geometrin.
Inom matematiken idag så är "matematiska objekt" och "matematiska rum" ofta synonymer.
Den minst generella och mest specifika av de geometrier som Klein relaterade till varandra var den euklidiska, vår vardagliga geometri.
Den mest generella geometrin är den projektiva geometrin, som jag tidigare har skrivit lite om.
Den projektiva geometrin fick ett uppsving i början av 1800-talet och var inte allmänt känd innan.
Erlangenprogrammet gjorde de olika geometrierna så nära besläktade med varandra att de bara kunde vara "sanna" och "falska" samtidigt.
Innan hade många frågat sej vilken som egentligen var den rätta geometrin bland alla dessa nya och gamla geometrier.
Alla dessa geometrier kan hittas i naturen.
Projektiv geometri beskriver t.ex skuggor och andra projektioner.
Erlangenprogrammet har haft ett enormt inflytande över stora delar av matematiken och även inom fysiken.
Innehållet är idag grundläggande självklarheter.
Ett annat namn för Erlangenskolan är Kleingeometri.
En generalisering är "Cartans geometri".
Cartans geometri användes bl.a för en tidig formulering av gravitationsteori.
Idag finns det fysiska teorier kring "observer space" som bygger på cartans geometri.
Alfred Tarskij höll 1966 ett föredrag som hette "What are logical notons?" där han föreslår en skiljelinje mellan logik och icke-logik som är inspirerad av erlangenprogrammet. Han blev mycket citerad.
När Saunders MacLane och Samuel Eilenberg skapade kategoriteorin 1945 så skrev de att:
"This may be regarded as a continuation of the Klein Erlanger Programm, in the sense that a geometrical space with its group of transformations is generalized to a category with its algebra of mappings"
Noether, som även var en föregångare till kategoriteorin, såg på matematiken som ett relationellt spel. inga talmängder utan konstruktionsmetoder.
Whitehead och Russell förenade logik med algebra och mängdlära, men geometrin och topologin ville inte passa in för Whitehead som istället skapade mereotopologin.
Inom kategoriteori så kan man nu jämföra algebra, logik, geometri och topologi.
Olika geometrier betraktas nu som grupper, enligt gruppteorin.
Kan det vara så att A.N. Whitehead inte kunde tämja geometrin för att han var otillräckligt bekant med gruppteorin och istället använde sej av mängdlära?
Hur imaginära är imaginära tal?
Alla kan vi räkna; 1, 2, 3 osv.
Men inte alla känner till att de där kallas för de naturliga talen.
Ska man bara använda naturliga tal så kan man räkna med plus och gånger men det kan bli problem om man vill använda minus eller delat med.
Tar man 2 minus 3 så får man t.ex inget "naturligt tal" utan ett "negativt tal".
De positiva och negativa heltalen kallas tillsammans för "integers".
Tar man 2 delat med 3 så får man inte heller något "naturligt tal", men inte heller en "integer".
Man får "2/3" som kallas för ett "rationellt tal", eftersom "ratio" ursprungligen betyder proportioner.
Försöker man att dela 10 med tre så kan reslutatet inte uttryckas fullständigt i decimalform eftersom man då vore tvungen att skriva oändligt många treor: "3,3333…". Däremot kan man skriva "10/3" vilket på sätt och vis är ett mer fullständigt svar.
Roten ur två kan däremot inte skrivas fullständigt varken som bråk eller i decimalform. Roten ur två innehåller oändligt många decimaler som inte upprepar sej. Sådana tal räknas inte till de rationella talen utan kallas för reella tal. Andra liknande tal är "e" och "pi". Alla rationella tal räknas som en del av alla reella tal. De reella talen som inte är rationella kallas för transcendentala.
Med hjälp av de reella talen kan vi nu göra alla möjliga matematiska beräkningar, utom en. Vi kan fortfarande inte ta roten ur minus ett. När man lär sig grundskolematte så får man ofta höra att det inte går att dra roten ur minus ett, och förklaringen verkar ju övertygande.
Ett negativt tal kan liknas vid ett hål.
Tag minus ett plus minus ett så får du ett dubbelt så djupt hål, alternativt två hål brevid varandra.
Ett minustecken innebär dock också att man gör något till sin absoluta motsats.
Tar man ett hål en gång så får man ett hål.
Tar man ett hål minus en gång så betyder det att man tar motsatsen till ett hål en gång och får ett positivt objekt istället.
Så minus ett gånger minus ett blir plus ett.
Man tycks inte kunna ta roten ur ett negativt tal.
Tar man ett tal gånger sej självt så får man alltid ett positivt svar.
När man insåg detta så insåg man dock också att man ibland behövde dra roten ur negativa tal. Vad är svaret på roten ur minus ett? En paradox.
Så man uppfann det imaginära talet. Men om ett negativt tal är ett hål, hur ser då ett imaginärt tal ut? Såväl objekt som hål kan beskrivas som sammanhang av relationer. Ett imaginärt tal måste också vara något sammanhang av relationer. Komplex matematik används ofta för att beskriva processer, inte minst periodiska funktioner. Ett komplext tal har en reell och en imaginär del. i är symbolen för det imaginära talet.
Vad negerar sej själv när man applicerar det på sej själv? Ljud och andra vibrationer negerar ju sej själva om de förskjuts på rätt sätt. Ett imaginärt tal materialiserat kanske blir en stående våg eller nått sånt. Vi har inte längre objekt och antiobjekt (hål) utan vågor. Enl. kvantfysiken så har alla partiklar både partikel- och vågegenskaper.
Vågorna slår mot stranden. Ibland är de där, ibland inte. De existerar genom att negera sej själva, annars vore de inte vågor. Oscilliationer är paradoxer utagerade i tiden.
Naturliga tal beskriver en värld av objekt.
Integers beskriver en värld av objekt och deras motsatser, som vi kan kalla "antiobjekt" eller "hål".
Rationella tal kan liknas vid objekt med delar.
Reella tal beskriver en kontinuerlig värld utan klara gränser mellan objekt. 0,9999…=1
Och beskriver komplexa tal en värld av vågor där objekt är specialfall av vågor?
Det komplexa planet är den första algebraiskt slutna mängden. Det finns ingen algebraisk uträkning som kräver mer än det komplexa planet. Detta kallas algebrans fundamentalsats.
De komplexa talen innefattar alla de övriga talmängderna och pekar inte nödvändigtvis vidare mot nya talmängder, som de tidigare talen gjorde. Det finns mer avancerade tal, "hyperkomplexa" tal som "quarternioner", men de har ganska liten praktisk användning medan komplexa tal har en mycket stor praktisk användning.
Komplexa tal kan beskriva rotation i två dimensioner mycket bra medan hyperkomplexa tal kan beskriva rotation i tre eller högre dimensioner. Hyperkomplexa tal har t.ex användning inom kvantfysiken.
Komplexa tal fångar bl.a vissa egenskaper hos trigonometri och används därför bl.a flitigt i sammanhang med trigonometriska funktioner, som fourieranalys, och bl.a i samband med elektricitet och magnetism. Komplex analys är en naturlig vidareutveckling av analys. Komplexa tal är också fundamentala för kvantmekanik. "Konformal maps" förenklar svåra ingenjörsproblem genom att tolka tredimensionella problem som tvådimensionella.
Förutom sin praktiska användning så förekommer det komplexa planet även flitigt inom högre matematik som mest intresserar matematiker.
Riemanns zätafunktion, elliptiska funktioner och betafunktionen hör till det komplexa planet.
Vissa fraktaler som mandelbrootmängden och juliamängderna hör till det komplexa planet.
Komplexa tal är via inverterad geometri kopplad till riemannsfären och kartografi.
En del människor envisas med att anse att endast de naturliga talen har någon fysisk eller metafysisk motsvarighet. Hade vi bara haft de naturliga talen så hade dock vår matematik fungerat mycket dåligt i verkligheten.
M-teorin och E11
När jag skrev om m-teorin så pekade jag på ett behov av ny matematik. Finns det då nånting inom den matematiska forskningens framkant som kan belysa den fysiska forskningens frontlinje?
Grothendiecks k-teori visade sej beskriva delar av m-teorin men inte hela.
Det finns dock nånting annat intressant. Minns ni killen som hittade kvantfältteorin i E8? Det vetenskapliga etablisemanget verkar inte ha intresserat sej så mycket, men det finns ett liknande projekt som kanske innefattar det första.
2001 kom någon på att E8s större släkting E11 tycks ha intressanta överrensstämmelser med m-teorin. M-teorin finns ju egentligen inte (ännu) men antas vara teorin som ligger bakom och förenar 5 olika strängteorier och en 11-dimensionell supergravitationsteori.
Det visar sej nu att E11 är en god kandidat för att göra just detta. I så fall så skulle m-teorin på något sätt vara identisk med E11, eller något liknande samband. Man håller dock ännu på att utforska E11 och ingen vill säga för mycket ännu. Det är ett mycket stort och komplicerat matematiskt objekt.
I så fall så skulle fysiken egentligen vara ett matematiskt objekt, i stil med ett nummer eller en triangel, fast mer komplicerat. E11 har oändligt många dimensioner och kallas för en Kac–Moody algebra.
På ett sätt så är E11 inte alls vad jag efterfrågade, eftersom jag ville ha någon ny matematik som skulle göra m-teorin mer hanterlig och praktisk, medan E11 mest bara verkar bekräfta att allt är oerhört komplcerat.
Man vet även att E12 existerar fast den vet man ännu mindre om.
Fouriertransformationen och du
Vilken matematik är det som fungerar i praktiken? Vilken typ av matematik beskriver bäst världen omkring oss?
När du hör ett ackord, tala om vilka toner som ingår. Detta är rätt exakt vad harmonisk analys är.
Världen omkring oss tycks ofta nå oss som en blandning av olika frekvenser. Därför är harmonisk analys en av de mest praktiska matematiska upptäckterna.
Den franske matematikern och fysikern Fourier upptäckte fouriertransformationen i början av 1800-talet när han sökte efter en formel för att beskriva spridningen av värme. Värme avtar kontinuerligt från värmekällan men med vissa plötsliga temperaturfall.
Fourier kom på att man kunde beskriva händelseförloppet genom att lägga samman sinusvågor av olika amplitud. Fourier var en frusen typ som eldade mycket hemma och hade många tillfällen att fundera över värmens spridning.
Fouriertransformationen kan användas på värmespridning, musik, ljus, ljud, vågor i allmänhet och även talteori. Allt detta kan kallas Fourieranalys eller harmoniska analys.
En matematisk funktion analyseras ner i flera delfunktioner, eller tvärtom så läggs flera funktioner ihop i en ny funktion.
Man kan skilja en informativ signal från rent brus och skenbart brus kan analyseras ner i flera begripliga funktioner. Så fourieranalys kan användas både i astronomi och geologi och allt där emellan.
Flera kontinuerliga funktioner kan tillsammans bilda en diskontinuerlig funktion.
Tänk "processer" eller "händelser" istället för funktioner.
Här sammarbetar "holism" och "analys".
Fouriertransformationer är närbesläktad med Laplacetransformationen och z-transformationen.
I "harmonisk analys" kan, förutom fouriertransformationen, även ingå isospektrala mångfalder m.m.
Kalkyl; dynamik och determinism
Jag hoppas att mina läsare har en vag aning om Zenons paradoxer från antikens Grekland. De gick ut på att på olika sätt bevisa att rörelse och förändring var en omöjlighet. Som t.ex "Akilles och sköldpaddan".
Akilles kan aldrig hinna ikapp sköldpaddan eftersom han alltid måste hinna halvvägs till skölpaddan först och i princip så finns det ett oändligt antal "halvvägs" som Akilles först måste förbi innan han hinner ikapp sköldis.
Aristoteles lösning var att ju kortare dessa avstånd var desto kortare tid att överbrygga dem. Detta är en bra ansats även om det inte fullbordar lösningen.
Grekernas matematik innehöll varken nollan eller oändligheten.
Om du tar ett steg som är 40 cm och sen ett steg som är 20 cm och sen ett steg som är 10 cm osv så kommer du aldrig att komma längre än 80 cm från utgångspunkten. Detta är gränsvärdet. En oändlig process ryms inom ett ändligt värde.
Insikten att en oändlg process kan leda fram till ett ändligt slutresultat är grunden för calculusen (och analysen).
Arkimedes tycks ha uppfunnit infinitesimaler och calculus redan under antiken, men detta glömdes bort och man var tvungen att uppfinna dem igen.
Viktiga principer återupptäcktes och vidareutvecklades av kineser och av muslimer men fick inget varaktigt inflytande.
Bonaventura Cavalieri, John Wallis, Isaac Barrow, James Gregory och Pierre de Fermat gjorde viktiga insatser innan Newton och Leibniz under sent 1600-tal började bråka om vem av dem som var först.
"Calculus" är en benämning på både differential- och integralkalkyler, som på ett sätt kompletterar varandra. Calculus beskrivs som en matematik för att beskriva förändring. Calculusen föreställer sej en oändlig process vilket senare skulle bli grunden för den matematiska analysen.
En differentialkalkyl räknar ut derivatan som är förändringshastigheten i ett ögonblick. En integralkalkyl räknar ut hur mycket som totalt har förändrats, t.ex hur mycket vatten som har runnit under bron. Calculus är förändringens matematik.
Förändring och framtid verkade nu bli nånting beräkningsbart och förutsägbart. Med calculusen införs både dynamik och determinism.
Newton och Leibniz räknas som calculusens uppfinnare. Deras dispyt är allmänt känd. Deras verk förenades av Euler, inte bara historiens mest produktive matematiker utan enastående på fler sätt än så. Euler och Cauchy skapade den matematiska analysen och funktionsläran (m.m.) Analys kallas alla oändliga matematiska processer. Analysen och funktionerna skulle få enorm praktisk betydelse. Utan Euler så hade ingenjörerna fått gå hem.
Newton såg i integralkalkylen en förening av rörelse och form, Liksom han i första mekaniska satsen jämställde likformig rörelse med att vara i vila, säkert inspirerad av galileisk relativitet.
Calculusen kopplades omgående till Descartes nya analytiska koordinatsystem. Om man har en kurva i en graf så kan man beräkna förändringshastigheten genom att räkna ut hur mycket kurvan lutar i en viss punkt. Det är lätt att räkna lutningen mellan två punkter och om man för dessa närmare varandra längs kurvan så når de till sist varandra.
Fast det är inte tillåtet. Punkterna måste komma så nära varandra som möjligt men de får inte förenas. Ju närmare punkterna kommer varandra så ser man dock snart att processen närmar sej ett gränsvärde.
Newton och Leibniz räknade dock istället med infinitesimaler, som ska vara mindre än något positivt tal men ändå större än noll.
Infinitesimalen kritiserades hårt av Berkeley i "The analyst" som kallade den "the ghosts of departed quantities." Hans kritik var i princip korrekt och infinitesimalerna togs senare bort och ersattes av gränsvärdesbegreppet. Ännu senare så återinfördes de igen.
Infinitesimalerna skulle kunna vara en inspiration för Leibniz monader. Försvinnande små entiteter som sammanfattar en utveckling.
Även mängden förändring under kurvan kan sammanfattas av en gränsvärdesprocess.
Genom att beskriva kvantitativ förändring på x-axeln och tiden på y-axeln banade man väg för att 250 år senare tolka tiden som den fjärde rumsdimensionen.
Calculus var den moderna matematikens första viktiga uppfinning. Idén om det oändligt lilla är här viktig. Calculus beskriver för första gången förändring och dynamik matematiskt.
Detta bidrog även till att göra determinismen populär.
Matematikern Laplace postulerade i slutet av 1700-talet ett tankeexperiment där en demon vet läget, hastigheten och riktningen hos varje partikel i universum och som därför borde kunna förutsäga framtiden för allt i universum, eftersom universum utvecklades enligt strikt deterministiska lagar.
Senare kopplades dynamiken till trigonometri när periodiska förändringar visade sej beskrivas av sin, cos och tan. I början av 1800-talet tycks Hegel beskriva sin dialektik som en sorts dynamisk trigonometri. Leibniz intresserade sej även för den kinesiska I CHING som enl. NE förutsäger "ödets cykliska förändringar".
I början av 1800-talet så varnade prästen Malthus för överbefolkningens domedag, vilket ingen dittills hade sett som något större problem. Enligt honom så utvecklades dock samhällets produktion linjärt medan befolkningsökningen följd en "geometrisk kurva" dvs nånting i stil med en andragradskurva. Så samhällets ökade produktion skulle aldrig kunna tävla med samhällets ökade behov. Enligt honom så stod mänsklighetens enda hopp till sexuell avhållsamhet och minskade barnkullar, men så var han också präst.
Hittills så har samhällets produktion mycket väl kunnat hålla jämna steg med befolkningsökningen. Problemet är snarare att vi lever i en ändlig värld med ändliga resurser och att tillväxten inte kan fortsätta för evigt.
Liknande tankar fanns i mitten av 1800-talet. Ekonomin kallade den pessimistiska vetenskapen därför att alla förutspådde att såväl vinst som tillväxt naturligt skulle komma att avta med tiden. Det fanns ett gränsvärde för ekonomisk tillväxt. J.S. Mill hoppades att när samhället i framtiden skulle tvingas att vänja sej vid att leva utan tillväxt så skulle förhoppningsvis ett annat samhälle kunna växa fram, ett mer stabilt och harmoniskt än dagens samhälle.
Marx ekonomiska uppfattningar påminnde om Mills och andra borgerliga ekonomers men Marx kombinerade brittisk ekonomi med tysk filosofi och fransk socialism. Under 1900-talet så har vi istället fått den eviga tillväxtens evangelium, ackumulation som religion.
Partiella integralfunktioner förenade det viktigaste hos matematiken och fysiken under hela 1800-talet. Detta har kallats den västerländska civilisationens höjdpunkt, när Europa behärskade världen och den vetenskapliga världsbilden började verka färdig.
Differentialgeometrin använder differentialkalkylens metoder på geometriska objekt. Differentialgeometrin inspirerade via Riemanns mångfalder topologins utveckling.
Även om calculus och analys på kort sikt främjade determinismen så upptäktes senare att inte alla system var förutsägbara ens om deras initialtillstånd var kända. Detta skulle leda till studier av kaotiska system; en ny nivå av dynamik. Även den nya kvantmekaniken underminerade determinismen. Sannolikhetskalkylen utvecklad av Pascal har istället fått bredare och bredare användningsområden.
Matematikens utveckling har gått från det statiska till det dynamiska, från det begränsade till det oändliga, från entydiga tillstånd till sannolikheter, från ordning till kaos, från det lågdimensionella till det högdimensionella, från det konkreta till det abstrakta.
lite om liegrupper och sånt
En mångfald, manifold, är ett topologiskt rum som är lokalt euklidiskt. Dvs alla objekt som är lokalt platta men som globalt kan vara andra former, som t.ex runda, är mångfalder. Det euklidiska rummet är en mångfald, liksom cirkeln och sfären.
Begreppet släta mångfalder, smooth manifolds, skapades av Riemann, i mitten av 1800-talet. En slät struktur innebär kontinuitet, som de reella talen, men inte de naturliga.
En slät mångfald är lokalt euklidisk, ungefär som jordklotet lokalt är platt, och liealgebra ersätter den globala "gruppen" med en lokal, linjär version, vilket gör det hela hanterbart.
Liegrupper är grupper som också är släta mångfalder, smooth manifolds. I ett ändligt, finit antal dimensioner. Så hilbertrymden som har ett infinit antal dimensioner är alltså ingen liegrupp. Däremot så är de reella talen en liegrupp, liksom enhetscirkeln.
Och denna smooth manifold är alltså sluten under en operation, för att få kallas grupp.
Groups innebär att man studerar förändringar inom en viss identitet, smooth manifold att dessa förändringar kan vara hur små som helst, och finit antal dimensioner innebär att detta inte tillhör den infinita matematiken.
Liegrupper visar sej vara mycket vanliga och finns i rikligt överallt inom matematiken och fysiken.
Euklides, Galilieis, Lorentz och Poincares symmetrigrupper är liegrupper.
Liegrupper är den bäst utvecklade teorin för kontinuerlig symmetri för matematiska objekt och strukturer vilket gör dem vanliga och oumbärliga inom matematik och fysik.
Liegrupper studerades först av Sophos Lie i slutet av 1800-talet. Han hade efter ett tag hjälp an Felix Klein som senare grundade erlangenprogrammet; ännu ett försök att hitta broar mellan olika delar av matematiken.
Lies tanke var att utveckla en teori om differentialekvationers symmetri som skulle klassifiera dem enligt gruppteori, liksom Galois hade gjort för algebraiska ekvationer.
Ungefär som geometriska former kan konstrueras matematiskt och studeras för sin egen skull så kan olika grupper och liegrupper konstrueras matematiskt och studeras för sin egen skull.
När liegrupper blir för stora så går de att dela upp i mindre liegrupper och liegrupper kan därför inte bli hur stora som helst, men de kan bli mycket stora. Exempel på gigantiska liegrupper är E8 och monstergruppen. E8 upptäcktes i slutet av 1800-talet.
E8 har nånting att göra med att packa bollar i åtta dimensioner på tätast möjliga sätt. Varje boll nuddar vid 240 andra bollar. Hela uträkningen av E8 är 60 gigabyte data vilket är ungefär i storleksordningen av en biblioteksvåning.
Herman Weyl jobbade med liegrupper inom fysiken under 1920 och 30-talen.
Eugene Wigner upptäckte så under 1930-talet en naturlig koppling mellan partikelfysik och representationsteori. Representationsteori handlar om linjära projektioner av t.ex grupper på vektorrum. Varje kvantpartikel ses som en representation av universums symmetrigrupp i hilbertrymden. Detta kan bl.a ge en matematisk "förklaring" till hel- och halvspinn. Representationsteori är ännu ett sånt där ämne som visar sej överallt inom matematiken och på många ställen inom fysiken också. Det finns representationsteori för Galilei, Lorentz och Poincarégrupperna.
Standardmodellen skapades bl.a utifrån Weyl och Wigners formuleringar. Liegrupperna SU(2) och SU(3) låg till grund för elektroweak interaction och quantum chromodynamics.
Group Field Theory är en quantum gravity teori som kombinerar en liegrupp med feynmandiagram och är nära besläktad med loop quantum gravity, casual dynamic triangulation och spin foam.
E8 har hittat användning inom strängteori och supergravitation. E8xE8 är en av de heterotiska strängteorierna.
E.S.T.E. är en utomakademisk TOE som akademikerna hittills har varit distanserade till trots att den håller hög matematisk nivå.
Monstergruppen har något att göra med att packa bollar i 24 dimensioner på tätast möjliga sätt. Den förutspåddes 1973 och konstruerades 1982.
1978 upptäcktes samband mellan monstergruppen och elliptiska modulära funktioner. Richard Boucherds bevisade monstrous moonshine förmodan 1998 och visade på djupa samband mellan elliptiska kurvor, monstergruppen och strängteori. Han använde sej av "no ghost"-teoremet från strängteori.
På ett ställe läste jag att monstergruppen har fler element än det finns atomer i Jupiter, på ett annat att den har fler element än det finns kvarkar i Solen. I vilket fall som helst så är det en skitstor grupp.
Såväl E8 som monstergruppen är avvikelser. Lite grann som primtal (och monstergruppen upptäcktes också via primtal.)
Många av undantagen inom matematik och fysik har visat sej ha förbindelser med varandra. E8 är förbunden med monstergruppen via modulära former, och bägge dessa har sina förbindelser med fysik.
Poincaré, topologi, Perelman

The mathematical facts worthy of being studied are those which, by their analogy with other facts, are capable of leading us to the knowledge of a physical law. They reveal the kinship between other facts, long known, but wrongly believed to be strangers to one another.
-Poincaré
The scientist does not study nature because it is useful; he studies it because he delights in it, and he delights in it because it is beautiful. If nature were not beautiful, it would not be worth knowing, and if nature were not worth knowing, life would not be worth living. Of course I do not here speak of that beauty that strikes the senses, the beauty of qualities and appearances; not that I undervalue such beauty, far from it, but it has nothing to do with science; I mean that profounder beauty which comes from the harmonious order of the parts, and which a pure intelligence can grasp.
-Poincaré
Poincaré var en naturbegåvning inom matematik och även den del andra fält. Han kallas ibland "den siste universalisten" inom matematik (vilket även andra har kallats). När han tog ett av de allra första intelligenstesterna som hans bekante Binet just höll på att utveckla, och fick ett resultat under medel, så ursäktade Binet honom med att matematikprofessorn nog hade haft annat att tänka på. Poincaré hade dålig syn och brukade för det mesta arbeta i huvudet.
Som tänkare var han ganska intuitiv och funderade sällan länge på ett problem innan han gick över till något annat och räknade med att hans undermedvetna skulle fortsätta att jobba på problemet.
Han ville se ett nära samband mellan matematik och fysik och var kritisk till den formalism som Hilbert stod för som en reaktion på Cantors infinita matematik. Mängdteori tyckte Poincaré illa om. Aritmetiken ansåg han vara syntetisk-apriori, liksom Kant.
Däremot vidareutvecklade han topologin och hjälpte till att befästa den som en viktig och central matematisk disciplin under 1900-talet. Topologin studerar former ungefär som geometrin, men utan exakta avstånd. En kvadrat ska ju t.ex ha lika långa sidor och nått sånt finns inte inom topologin. Istället pekar topologer på likheterna mellan kvadrater, trianglar och cirklar, t.ex.
Dessa kan sägas vara "homologa" genom att man t.ex kan forma ett gummiband till dessa olika former, utan att klippa eller klistra i gummibandet. Egentligen är alla objekt homologa som har samma antal hål i sej; så ett "B" är homologt med en "8" osv. "Homotopi" är ungefär samma sak som "homologi"; skillnaden är något för utbildade matematiker att hålla reda på.
Vill man ha lite större likhet mellan objekt så kan topologer istället tala om "homomorfism". "Topologiska objekt" är nästan samma sak som "topologiska rum" och objekt kan även vara så komplexa att de är oavgörbara och man kan t.ex inte räkna hålen i dem.
Även grafteori och knutteori räknas som delar av topologin. Topologin fick tidigt praktisk användning inom elektronik och kemi.
En del hävdar att Poincaré var före Einstein med relativitetsteorin. Redan år 1900 publicerade han en formel som är nästan identisk med E=mc2 och 1902 publicerade han en populärvetenskaplig bok där han tog upp en del saker han jobbat med och som förebådade Einsteins publiceringar från 1905.
Trots att han skrev om möjligheten att det inte fanns något absolut rum eller absolut tid och att etern inte existerade så fortsatte Poincaré att förutsätta dessa i sina beräkningar och därför så räknas Einstein som den som upptäckte den egentliga relativiteten.
Poincaré fick idén att göra en fyrdimensionell modell av rum och tid, vilken sedan förverkligades av Minowski, och Poincaré gjorde och så ett tidigt försök att omformulera Newtons gravitation inom en relativistik ram.
All kvantfysik och relativitetsteori tycks utspela sej inom Poincaregruppen, som är en symmetrigrupp: "om detta ändras så ändras även det här". Ett specialfall av poincaregruppen är Lorentztransformationerna.
Poincaré undersökte om solsystemet var stabilt eller instabilt men detta var svårt att räkna ut. Han undersökte tre-kroppars-problemet och blev därmed en föregångare till kaosteoretikerna.
Poincarés förmodan var att precis som sfären är den enklaste formen i våra vanliga tre dimensioner och alla lika enkla former kan kontinuerligt omformas till sfärer av topologer, så gäller även samma sak i högre dimensioner.Perelman visade att detta mycket riktigt stämde. Liksom Poincaré så var även Perelman duktig inom både fysik och matematik.
När Perelman visade lösningen så var det en kombination av olika tekniker från olika matematiska discipliner, vilket gjorde mer renläriga topologer besvikna. De hade hoppats på en mer ren topologisk lösning. Kanske var det delvis därför som problemet hade tagit så lång tid att lösa. Många matematiker är bara specialister på sitt eget fält.
Perelman gjorde sitt bästa för att bekräfta bilden av framstående matematiker som galna genier, genom att tacka nej till pris, pengar och intervjuer och bo kvar hemma hos sin mamma.
Det finns ingen praktisk anvädning av denna kunskap idag men matematiker tycker att det är en stor och viktig insikt.
Det finns en koppling till kosmologi dock. Om man drog en tråd genom hela universum och kom tillbaka till samma ställe och knöt ihon ändarna, skulle man då kunna dra in hela tråden och samla den på samma ställe? Eller finns det ett eller flera topologiska hål i universums form som skulle få tråden att fastna?
Man övervägde faktiskt att universum skulle kunna ha dodekaeder-symmetrisk form, men denna obskyra matematiska möjlighet verkar nu vara övergiven.

lite om differentiell geometri och fysik
Gauss, ibland kallad matematikernas kung, skapade den differentiella geometrin när han 1828 råkade skapa theorema egregium som visade att man kan bestämma en ytas krökning som en intrinsikal egenskap hos själva ytan utan hänvisning till det omkringliggande rummet.
Om man tittar på en form så är det lätt att se om dess yta är krökt eller platt. Då ser man ytan och formen i rummet. Men vad Gauss gör med theorema egregium är att han blundar och stäcker fram handen och känner på ytan. Hur känns själva ytan? Känns den krökt? Man känner bara relationen mellan olika delar av ytan och tillsamman gör dessa att ytan känns krökt.
Med hjälp av matematik från integral och differentialekvationer så kan man jobba med geometriska former på ett nytt sätt. Detta kallas differentialgeometri. Enbart genom att bestämma avstånd och vinklar på själva ytan så kan man bestämma om ytan är krökt i rummet, utan att matematiskt undersöka ytans krökning i rummet. Man känner bara på ytan, utan att titta.
Differentialgeometrin är viktig för kartprojektioner och förklarar varför ingen platt karta kan återge ytan på en tredimensionell sfär som Jorden. På en sfär så kan man t.ex skapa en triangel med enbart räta vinklar. Det är omöjligt på en plan yta.
Tydligen så är det även differentialgeometrin som förklarar varför en trekantig pizzaslize blir styv om man böjer upp kanterna en aning, och därför lättare att äta.
Riemann närvarade vid några föreläsningar av Gauss och från 1854 började Riemann lägga grunden till riemanngeometri som är en förutsättning för Einsteins relativitetsteori. Riemanngeometri kan räknas som en del av differentialgeometrin.
Differentialgeometri används inom relativitetsteori och inom gaugeteori och även av Perelman när han bevisade Poincares förmodan (genom att hantera universum som en mozarellapizza).
Hermann Weyl (som hade samma älskarinna som Schrödinger) skapade gaugeteorin 1918 (bl.a influerad av Husserls fenomenologi) i ett då misslyckat försök att förena elektromagnetism med gravitationsteori. Gaugeteorin skulle dock överleva och vidareutvecklas.
Under 40- och 50-talen så utvecklade fysikerna gaugefältteorier. Samtidigt så utvecklade matematikerna den differentiella geometrin med begrepp som "vector fields" och "fibre bundles" m.m. Under tidigt 1970-tal så upptäckte man oväntade samband mellan dessa olika forskningsfält. De verkade vara två varianter av samma sak. Likheterna var påtagliga.
Även matematiken influerades av fysiken. Matematiska idéer från gaugeteori inspirerade den uppmärksammade upptäckten av "exotiska strukturer" på den fyrdimensionella riemannsfären 1984. Dvs när en sfär är fyradimensionell så skapas det av någon anledning extra information. Detta skulle kanske kunna ha något med fysiken i vårt universum att göra men området verkar inte vara speciellt uforskat.
18 mars 2010 kungjordes att ryssen Perelman hade löst Poincares förmodan. Han använde sej bl.a av "ricci flow" från differentiell geometri. Men mer om det i en annan postning.
The more things change, the more they remain the same

Tänk dej att jag fotograferar flera olika objekt sett från olika håll och att du sedan ska försöka gruppera fotografierna efter de olika objekt som de visar. Känner du igen objekten så kan det vara lätt, känner du inte igen objekten så kan det vara svårt.

I evigheters evighet


Lite bättre.

Matematiker emellan
Why we think like quirks
A pluralistic universe

Filosofins matematik

Trigonometrin är med Pythagoras sats en av de allra äldsta disciplinen inom matematiken, men den hade inkorporerats i den komplexa analysen av Euler från 1748 till 1782. Hegel studerade trigonometri 1787, sfärisk dessutom, när han var 17 år gammal och hans senare filosofi har några likheter med trigonometri. Inom trigonometri arbetar man med tangent, sinus och cosinus. Har man två sidor kan man räkna ut den tredje, har man två vinklar kan man räkna ut den tredje. Sin, cos och tan används även för att räkna ut regelbundna svängningar. Därav t.ex uttrycket "sinusvåg". Så tre element leder alltså fram till en periodisk svängning mellan extremer i en historisk utveckling. Ungefär som i Hegels filosofi.
Whitehead skapade den punktfria mereotopologin som enligt honom själv är en viktig del av av hans "organic philosophy", eller "processfilosofi" som den brukar kallas.
Pointless?
Projektiv geometri

