Tempus Fugit

Redan de gamla grekerna funderade över kontinuiteten. Zenon med paradoxerna visade att antagandet att rummet var oändligt delbart ledde till märkliga konsekvenser, som att förändring och rörelse var omöjligt.

Inom nutida matematik och fysik så ställer kontinuiteten också till med problem.

Det kan ha varit Erdmann eller någon annan tysk filosofihistoriker som jag läste för kanske 15 år sen, som satte antik filosofi, speciellt grekisk, mot modern filosofi, speciellt tysk. Medan antik filosofi hade som övergripande ideal den välformade kroppen, anatomisk eller matematisk eller annan, så har den moderna filosofin oändligheten som ideal. För de antika var det oändliga obegränsat, oformat, laglöst och ont. Allt med måtta, var idealet.

Oswald Spengler gör en liknande uppställning i Västerlandets undergång, även om han skiljer mellar fler än två olika kulturer. Mellan antiken och moderniteten ser han t.ex den arabiska och den medeltida kulturen. Enligt honom har varje kultur en unik matematik. Den moderna oändlighetstanken spårar han tillbaka till gotiska katedraler och gregoriansk kyrkosång. Där finns enligt Spengler rötterna till den moderna matematiken.

Aczel skriver i The mystery of the Aleph om hur oändligheten blev grunden för den moderna matematiken iom Cantor och Zermelo. Amir D Aczel spårar oändlighetstanken tillbaka till Zenons paradoxer och till pythagoreerna som upptäckte de irrationella talen. Han skriver även om oändligheten hos medeltida kabbalister vilket visar sig vara en direkt influens för Cantor.

Galileo var den förste matematikern som kom fram till något faktiskt forskningsresultat rörande faktisk oändlighet när han i Om två nya vetenskaper (1638) bevisade att mängden av alla heltal var lika stor som mängden av kvadraterna på alla heltal. Vilket intuitivt låter som en paradox.

Infinitesimalkalkylen och gränsvärdesbegreppet räknar med värden som går mot oändligheten. Den matematiska analysen använder sej av oändliga processer. Infinitesimaler kritiserades redan av Berkeley m.fl (och lustigt nog även av Cantor).

Mängdteori, set theory,  behöver inte alls arbeta med oändligheter, men det var därför som Cantor uppfann den. Hans första och sista problem var kontinuiteten, de reella talen. Hans stora upptäckt var att det fanns oändligheter av olika storlek. Kontinuitetens problem löste han dock inte. Mängdteori blev fort väldigt kontroversiell. Såväl den matematiska intuitionismen som finitismen kan sägas ha skapats i opposition till den.

Cantor arbetade på mängteorin från 1874 till 1897. Han bevisade i den första artikeln att det fanns mer än en oändlighet. Såväl mängdbegreppet som oändlighet var känt tidigare men ingen hade gjort någon djupare studie i dessa begrepp. Man antog att de var triviala. I sitt sista arbete så hade han velat bevisa kontinuumhypotesen (CH), men fick nöja sej med att beskriva well-ordered sets och ordinal numbers. Med hjälp av dessa begrep kunde man använda transfinit induktion.

CH var det första av Hiberts 23 problem som han publiserade 1900. Ungefär samtidigt så löste Planck en oändlighetsparadox inom fysiken genom att införa ett begrepp om energikvanta. Samtidigt som Cantor fördjupade kontinuitetsmatematiken så övergick Planck från kontinuitetsmekaniken till kvantmekaniken. Även diskontinuerlig matematik, discomatte, har blivit populärt iom datorernas framväxt.

1899 åkte Cantor in på hospital för andra gången och blev efter det sämre och gjorde inte mycket inom matematik längre. Han tycks ha haft en manodepressiv läggning, hade en del religiösa grubblerier och plågades av illvilliga fiender till sitt arbete. Han dog fattig och undernärd på ett hospital 1918, 73 år gammal. Han hann ändå uppmärksammas och hyllas under sin livstid, t.ex av CS Peirce som själv hade varit inne på liknande tankar, men det var för lite för sent och vägde inte upp för attackerna mot honom.

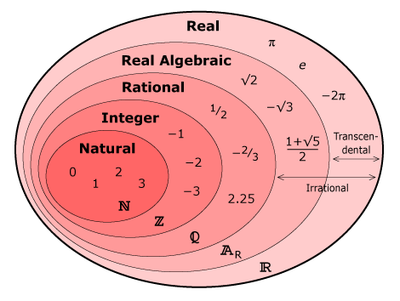
Jag har sett roligare Venn-diagram.

1904 skapade Ernst Zermelo axiom of choise (AC). AC är ekvivalent med wellordering theorem och Zorns lemma. 1905 började Zermelo att axiomatisera mängdteorin. 1922 föreslog två andra forskare oberoende av varandra förbättringar på hans axiom  vilket resulterade i Zermelo-Fraenkel set theory (ZF), den mest använda varianten. Om AC ska finnas med så blir förkortningen ZFC.

"The Axiom of Choice is obviously true, the well-ordering principle obviously false, and who can tell about Zorn's lemma?"

— Jerry Bona

Detta är ett skämt som går ut på att många matematiker tycker att AC känns rätt, WoP känns fel och Zorn´s lemma känns omöjligt att avgöra, trots att de bara kan vara sanna och falska samtidigt.

AC tycks ha att göra med att man måste börja någonstans. Det måste finnas en början, ett första tal. T.ex det minsta talet. Men när man räknar oändligheter, vilken oändlighet är då minst? Ett kardinaltal är en oändlighet. Utan AC så kan man inte göra transfinit matematik.

Kurt Gödel visade 1940 att både AC och CH är förenliga med ZF. (Detta betydde inte att han själv gillade CH eller ZF.) Paul Cohen upptäckte 1963 med sin nya metod att varken CH eller AC är bevisbart inom ZF. Tillsammans med Gödels tidigare forskning så visade det att CH och AC bägge är oberoende av ZF, och att man kan lägga till eller ta bort dom som man vill.

Kontinuitetens problem är ännu olöst idag. Att säga att det finns oändligt många punkter i en linje är inte särskilt exakt eftersom det anses finnas oändligt många oändligheter. Vilken oändlighet som motsvara antalet punkter i en linje vet man inte. Åtminstone vissa matematiker tycker att detta är ett stort och viktigt problem att lösa inom matematiken. Ännu idag kan matematik med oändligheter väcka ganska starka reaktioner, inte minst emot. Cantor hade rätt så passionerade fiender bland andra matematiker.

Både Gödel och Cohen misstänker att CH är falsk. Två andra matematiker har lagt fram indicier mot CH. Vad betyder det? En kontinuerlig linje innehåller oändligt många punkter, men vi vet idag inte vilken oändlighet. CH utgör ett minimiförslag. Andra alternativ gör kontinuumet mycket större. Nyligen publicerades en bok som argumenterade för ännu större oändligheter, just med hänvisning till kontinuitetsproblemet.

Paul Cohen dog 23/3 - 2007. Jag tänkte skriva något redan då men det har inte blivit av förrän fyra år senare.

1903 höll Cantor en föreläsning om paradoxer inom transfinit matematik. Dessa paradoxer har ofta framhållits som kritik av hans projekt.

Det finns flera olika mängdteorier/set theories. Inte alla leder fram till paradoxer. Även mereologi påminner om mängdlära och har inte Russells paradox.

Den sk. krisen för matematikens fundament kring 1900 uppstod för att grundläggande antaganden ledde till paradoxer som verkade mycket svåra att få bort. Krisen är egentligen inte löst idag utan man navigerar i praktiken runt paradoxerna. Matematik är snarare nånting som fungerar i praktiken än ett perfekt system av intern motsägelsefrihet. Transfinita idéer kan användas praktiskt inom en del programmering, annars är detta ren grundforskning för kunskapens egen skull.

Det finns även matematik som går ut på att utforska paradoxala antaganden för att undersöka vilken blandning av ordning och kaos som de leder till.

Cantor blev galen mot slutet, liksom även andra som har jobbat med oändligheten inom matematiken. Problemet ska dock inte romantiseras eller mystifieras som Aczel gör. Man löser inga svåra intellektuella problem genom att sitta och stirra på ett tomt ark i år och decennier. Svåra intellektuella problem löser man på andra sätt. Feynman kollade t.ex på stripshower och rökte braj och det funkade bra för honom.

Cantor var bevisligen influerad av mystiska och religiösa tankegångar när han uppfann mängdläran. Förutom från andra matematiker så fick han även en del vass kritik från teologer, vilket inte var oviktigt för honom.