Tempus Fugit

Planck började forska i svartkroppsstrålningen 1894. I oktober 1900 kom han fram till sin första version av Plancks svartskroppsstrålningslag. I november 1900 så omarbetade han sin teori och trots sitt motstånd mot statistisk mekanik så bestämde han sej för att använda Boltzmanns statistiska tolkning av termodynamikens andra lag, och trots att han var misstänksam mot följderna, men han såg ingen annan möjlighet.

14e december 1900 presenterade han sin nya tolkning och det centrala antagandet var att elektromagnetisk energi bara kunde utstrålas i kvantifierad form. Detta antagande var oförenligt med fysiken dittills och anses vara födelsen av kvantfysiken. Den konservative Planck hade startat 1900-talets stora revolution inom det alltmer stangerade ämnet fysik. Själv ville han först bara se det som ett teoretiskt arrangemang.

Tidigare nämnde Boltzmann hade 1877 diskuterat den rent teoretiska möjligheten av att fysiska system skulle kunna ha diskreta energitillstånd. Plancks arbete vidareutvecklades av Einstein i hans arbete om den fotoelektriska effekten 1905. Han uppfann begreppet "foton" för en ljuspartikel. Thomas Kuhn har föreslagit att det snarare var Einstein än Planck som skapade kvantfysiken eftersom Einstein i högre grad förståd vad han bidrog till, än vad Planck gjorde.  Einstein var den förste som sa att Plancks kvanta skulle reformera hela fysiken. Det hade dock varit krångligare att tala om Boltzmann-Einstein-konstanten än om Planck-konstanten. (och Boltzmann har ju redan en konstant.)

Planck förstod dock kvickt betydelsen av Einsteins relativitetsteori, också 1905, och hjälpte till att göra den populär. Plack hjälpte till att göra Einstein till professor 1914 och snart därefter så träffades de och blev vänner privat.

Niels Bohr kombinerade kvantprinciperna med den bästa tillgängliga atommodellen, Rutherfords från 1911, och fick Bohr-modellen av atomen som publicerades 1913.

Bohr grundade 1921 institutet för teoretisk fysik, med bidrag från Danska staten och Carlsbergfonden. Bohr fick en central roll i det internationella sammanhanget av fysiker. Bohr och Einstein blev de två motpolerna inom forskningen där Einstein stod för det realistiska lägret och Bohr för det instrumentalistiska.

Fram till 1924 fokuserades forskningen kring något som idag kallas den gamla kvantteorin, som byggde på Bohr-modellen. !924 publicerade De Broglie något som förändrade detta. Han blev sedemera fransk hertig och hade först tänkt bli humanist.

"The fundamental idea of [my 1924 thesis] was the following: The fact that, following Einstein's introduction of photons in light waves, one knew that light contains particles which are concentrations of energy incorporated into the wave, suggests that all particles, like the electron, must be transported by a wave into which it is incorporated... My essential idea was to extend to all particles the coexistence of waves and particles discovered by Einstein in 1905 in the case of light and photons."

"When I conceived the first basic ideas of wave mechanics in 1923-24, I was guided by the aim to perform a real physical synthesis, valid for all particles, of the coexistence of the wave and of the corpuscular aspects that Einstein had introduced for photons in his theory of light quanta in 1905."

Med detta blev de Broglie den egentliga skaparen av vågmekaniken inom kvantfysiken. Själv hade han en realistisk tolkning av sin hypotes, där materievågorna var något lokalt, reellt, i någon mening materiellt, som följde med alla partiklar. Hans matematik kunde dock tolkas på andra sätt. de Broglie hade flera djupgående hypoteser under sin karriär men dem tar vi inte just nu.

Opponenterna hade för säkerhets skull rådfrågat Einstein som var den som egentligen godkände hypotesen. Snart utvidgade han de Broglies ursprungliga vågekvation till en mer klassisk materievåg.

1925 skapade Heisenberg matrix-mekaniken som en annan formulering av vågmekaniken. Matrix-mekaniken räknas som den första självständiga och sammanhängande teorin inom kvantmekanik och Heisenberg fick Nobelpriset "… for the creation of quantum mechanics …".

Man kan säga att Heisenbergs matrix-mekanik var en mycket mer abstakt tolkning av kvantmekaniken än de Broglies. Verkligheten är ju inte i sej en matematisk matris. Matrix-mekaniken var en instrumentalistisk skapelse.

Längre hann jag inte just nu. Jag har bl.a kämpat med ett magvirus. Fortsättning följer.

andra bloggar om

fysik, kvantfysik, kvantmekanik, vetenskapshistoria,

Redan de gamla grekerna funderade över kontinuiteten. Zenon med paradoxerna visade att antagandet att rummet var oändligt delbart ledde till märkliga konsekvenser, som att förändring och rörelse var omöjligt.

Inom nutida matematik och fysik så ställer kontinuiteten också till med problem.

Det kan ha varit Erdmann eller någon annan tysk filosofihistoriker som jag läste för kanske 15 år sen, som satte antik filosofi, speciellt grekisk, mot modern filosofi, speciellt tysk. Medan antik filosofi hade som övergripande ideal den välformade kroppen, anatomisk eller matematisk eller annan, så har den moderna filosofin oändligheten som ideal. För de antika var det oändliga obegränsat, oformat, laglöst och ont. Allt med måtta, var idealet.

Oswald Spengler gör en liknande uppställning i Västerlandets undergång, även om han skiljer mellar fler än två olika kulturer. Mellan antiken och moderniteten ser han t.ex den arabiska och den medeltida kulturen. Enligt honom har varje kultur en unik matematik. Den moderna oändlighetstanken spårar han tillbaka till gotiska katedraler och gregoriansk kyrkosång. Där finns enligt Spengler rötterna till den moderna matematiken.

Aczel skriver i The mystery of the Aleph om hur oändligheten blev grunden för den moderna matematiken iom Cantor och Zermelo. Amir D Aczel spårar oändlighetstanken tillbaka till Zenons paradoxer och till pythagoreerna som upptäckte de irrationella talen. Han skriver även om oändligheten hos medeltida kabbalister vilket visar sig vara en direkt influens för Cantor.

Galileo var den förste matematikern som kom fram till något faktiskt forskningsresultat rörande faktisk oändlighet när han i Om två nya vetenskaper (1638) bevisade att mängden av alla heltal var lika stor som mängden av kvadraterna på alla heltal. Vilket intuitivt låter som en paradox.

Infinitesimalkalkylen och gränsvärdesbegreppet räknar med värden som går mot oändligheten. Den matematiska analysen använder sej av oändliga processer. Infinitesimaler kritiserades redan av Berkeley m.fl (och lustigt nog även av Cantor).

Mängdteori, set theory,  behöver inte alls arbeta med oändligheter, men det var därför som Cantor uppfann den. Hans första och sista problem var kontinuiteten, de reella talen. Hans stora upptäckt var att det fanns oändligheter av olika storlek. Kontinuitetens problem löste han dock inte. Mängdteori blev fort väldigt kontroversiell. Såväl den matematiska intuitionismen som finitismen kan sägas ha skapats i opposition till den.

Cantor arbetade på mängteorin från 1874 till 1897. Han bevisade i den första artikeln att det fanns mer än en oändlighet. Såväl mängdbegreppet som oändlighet var känt tidigare men ingen hade gjort någon djupare studie i dessa begrepp. Man antog att de var triviala. I sitt sista arbete så hade han velat bevisa kontinuumhypotesen (CH), men fick nöja sej med att beskriva well-ordered sets och ordinal numbers. Med hjälp av dessa begrep kunde man använda transfinit induktion.

CH var det första av Hiberts 23 problem som han publiserade 1900. Ungefär samtidigt så löste Planck en oändlighetsparadox inom fysiken genom att införa ett begrepp om energikvanta. Samtidigt som Cantor fördjupade kontinuitetsmatematiken så övergick Planck från kontinuitetsmekaniken till kvantmekaniken. Även diskontinuerlig matematik, discomatte, har blivit populärt iom datorernas framväxt.

1899 åkte Cantor in på hospital för andra gången och blev efter det sämre och gjorde inte mycket inom matematik längre. Han tycks ha haft en manodepressiv läggning, hade en del religiösa grubblerier och plågades av illvilliga fiender till sitt arbete. Han dog fattig och undernärd på ett hospital 1918, 73 år gammal. Han hann ändå uppmärksammas och hyllas under sin livstid, t.ex av CS Peirce som själv hade varit inne på liknande tankar, men det var för lite för sent och vägde inte upp för attackerna mot honom.

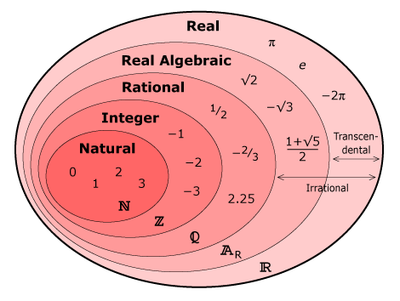
Jag har sett roligare Venn-diagram.

1904 skapade Ernst Zermelo axiom of choise (AC). AC är ekvivalent med wellordering theorem och Zorns lemma. 1905 började Zermelo att axiomatisera mängdteorin. 1922 föreslog två andra forskare oberoende av varandra förbättringar på hans axiom  vilket resulterade i Zermelo-Fraenkel set theory (ZF), den mest använda varianten. Om AC ska finnas med så blir förkortningen ZFC.

"The Axiom of Choice is obviously true, the well-ordering principle obviously false, and who can tell about Zorn's lemma?"

— Jerry Bona

Detta är ett skämt som går ut på att många matematiker tycker att AC känns rätt, WoP känns fel och Zorn´s lemma känns omöjligt att avgöra, trots att de bara kan vara sanna och falska samtidigt.

AC tycks ha att göra med att man måste börja någonstans. Det måste finnas en början, ett första tal. T.ex det minsta talet. Men när man räknar oändligheter, vilken oändlighet är då minst? Ett kardinaltal är en oändlighet. Utan AC så kan man inte göra transfinit matematik.

Kurt Gödel visade 1940 att både AC och CH är förenliga med ZF. (Detta betydde inte att han själv gillade CH eller ZF.) Paul Cohen upptäckte 1963 med sin nya metod att varken CH eller AC är bevisbart inom ZF. Tillsammans med Gödels tidigare forskning så visade det att CH och AC bägge är oberoende av ZF, och att man kan lägga till eller ta bort dom som man vill.

Kontinuitetens problem är ännu olöst idag. Att säga att det finns oändligt många punkter i en linje är inte särskilt exakt eftersom det anses finnas oändligt många oändligheter. Vilken oändlighet som motsvara antalet punkter i en linje vet man inte. Åtminstone vissa matematiker tycker att detta är ett stort och viktigt problem att lösa inom matematiken. Ännu idag kan matematik med oändligheter väcka ganska starka reaktioner, inte minst emot. Cantor hade rätt så passionerade fiender bland andra matematiker.

Både Gödel och Cohen misstänker att CH är falsk. Två andra matematiker har lagt fram indicier mot CH. Vad betyder det? En kontinuerlig linje innehåller oändligt många punkter, men vi vet idag inte vilken oändlighet. CH utgör ett minimiförslag. Andra alternativ gör kontinuumet mycket större. Nyligen publicerades en bok som argumenterade för ännu större oändligheter, just med hänvisning till kontinuitetsproblemet.

Paul Cohen dog 23/3 - 2007. Jag tänkte skriva något redan då men det har inte blivit av förrän fyra år senare.

1903 höll Cantor en föreläsning om paradoxer inom transfinit matematik. Dessa paradoxer har ofta framhållits som kritik av hans projekt.

Det finns flera olika mängdteorier/set theories. Inte alla leder fram till paradoxer. Även mereologi påminner om mängdlära och har inte Russells paradox.

Den sk. krisen för matematikens fundament kring 1900 uppstod för att grundläggande antaganden ledde till paradoxer som verkade mycket svåra att få bort. Krisen är egentligen inte löst idag utan man navigerar i praktiken runt paradoxerna. Matematik är snarare nånting som fungerar i praktiken än ett perfekt system av intern motsägelsefrihet. Transfinita idéer kan användas praktiskt inom en del programmering, annars är detta ren grundforskning för kunskapens egen skull.

Det finns även matematik som går ut på att utforska paradoxala antaganden för att undersöka vilken blandning av ordning och kaos som de leder till.

Cantor blev galen mot slutet, liksom även andra som har jobbat med oändligheten inom matematiken. Problemet ska dock inte romantiseras eller mystifieras som Aczel gör. Man löser inga svåra intellektuella problem genom att sitta och stirra på ett tomt ark i år och decennier. Svåra intellektuella problem löser man på andra sätt. Feynman kollade t.ex på stripshower och rökte braj och det funkade bra för honom.

Cantor var bevisligen influerad av mystiska och religiösa tankegångar när han uppfann mängdläran. Förutom från andra matematiker så fick han även en del vass kritik från teologer, vilket inte var oviktigt för honom.

Historiskt har flera försök gjorts att skapa en förenande teori för matematiken och även framstående matematiker har uttryckt önskemål åt detta håll. Liksom inom fysiken önskas en Grand Unified Theory.

Idag fungerar mängdlära som en övergripande eller grundläggande teori för matematiker. Den har dock "utmanats" av kategoriteori.

Det finns också mer partikulära brobyggen mellan specifika områden, ett-till-ett-korrespondens, som även de kan få betydande följder. Descartes visade att geometrin kunde uttryckas algebraiskt, vilket några hundra år senare ledde fram till Hilberts Nullstellensatz.

Galoisteori nämns även och Andrew Wiles använde Galois arbete som en grundsten när han 1993 bevisade Taniyama-Shimuras förmodan, som ursprungligen förmulerades 1955 och som knöt samman två vitt skilda områden inom matematiken.

Taniyama-Shimuras förmodan är viktig både för Langlandsprogrammet (skapat 1967) och för något som kallas för monsterous moonshine. Såväl Fieldspriset 2002 som 2010 går till arbeten relaterade till Langlandsprogrammet. Robert Langland föreslog en större mängd samband inom matematik som ännu återstår att bevisa.

En del av resultaten inom Langlandsprogrammet har varit av intresse för fysiker; m-teoretiker och andra.

En viktig poäng med att kunna hitta korrespondenser mellan skilda discipliner är att svåra nötter inom en disciplin kan visa sej lättare att knäcka när de översätts till en annan disciplin.

andra bloggar om

matematik,

Nästan inget är känt om Nagarjunas liv med säkerhet även om det finns flera myter och legender. Han räknas som en av de allra viktigaste filosoferna och skolbildarna inom buddhismen. I hans namn finns "Naga" - den visa kobran. Han ska ha varit född i södra Indien som hindu i en brahminfamilj men konverterade senare till buddhismen. Han ska även ha varit bekant med en lokal kung vilket placerar hans livstid till nån gång mellan 150-250 ekr.

Genom att förespråka den gyllenne medelvägen så tycks han ha velat motverka sekterism inom buddhismen men istället så råkade han indirekt orsaka den största splittringen av dem alla - den mellan theravada och mahayana. Visserligen så fanns det ansatser till mahayanabuddhism redan innan Nagarjuna men hans madhyamikaskola räknas som mahayanabuddhismens äldsta filosofi. Och Nagarjuna som bara ville återupprätta Buddhans ursprungliga lära.

Den Gyllenne Medelvägen är en tanke som återfinns både inom buddhism och inom aristotelism. Det finns åtminstone vissa vaga likheter mellan buddhism och aristotelism:

Aristoteles var en slags hedonist som hävdade att meningen med livet var lycka. Buddhister hävdar att "allt är lidande" och att "lidandet går att upphäva". En slags negativ hedonism, alltså.

För Aristoteles så består allting av form och materia, och ren materia är helt egenskapslöst. För buddhister så består allting av form och "tomhet", och "tomhet" är något ovetbart.

Medan Aristoteles grundlade den västerländska logiken som vetenskap så var buddhister framstående inom österländsk logik. Nagarjuna accepterade dock inte den etablerade logiken.

Tetralemmat återfinns i antik grekisk logik;

för en proposition så finns det fyra alternativ:

ja, nej, både ja och nej samt varken ja eller nej.

I Indien så fanns något liknande: catuskoti.

Buddhistisk logik kom att fokusera på detta.

Nagarjuna däremot är känd för att han hävdar ett femte alternativ som inte är något av de fyra nämnda alternativen.

Frågan som diskuterades är om något finns. Buddhismen skiljde sej från hinduismen genom att hävda att allt är tomt. Allt är en illusion därför att det inte har någon varaktig existens. Likaså hade människan inte en odödlig själ (atman) utan en icke-själ (anatman) och när man till sist nådde nirvana så innebar detta inte att nå tillvarons fullhet utan tillvarons tomhet. Alla dessa trossatser debatterades och tolkades på olika sätt inom buddhismen.

Nagarjuna ville visa teoretiserandets fåfänglighet. Att tillvarons sanning var tomhet innebar inte att ingenting finns. Inte heller att någonting finns. Inte heller att nånting både finns och inte finns. Inte heller att nånting varken finns eller inte finns. När man hade lagt de alternativen åt sidan så hade man kommit fram till sanningen: tomhet.

Hans skiljde mellan konventionell och faktisk sanning men ingenting hamnade i den senare kategorin. Allt var bara tomma åsikter. Han uttryckte att även (buddhismens) tomhet var något tomt. Han skrev även att om man skapade en lära av hans skrifter så hade man missförstått honom helt. Ickedestomindre har begreppet "tomhet", sunya, efter honom kommit att bli grundläggande inom buddhistisk filosofi.

Nagarjunas icke-dualistiska skola, Madhyamika, intar en mellanposition, den gyllenne medelvägen,  mellan att något finns (hinduism) och att inget finns (buddhism). I sin konsekventa buddhism är den alltså lika postbuddhistisk som posthinduistisk. Nagarjuna förnekar oxå anatman-teorin liksom skillnaden mellan samsara och nirvana. Inom vissa esoteriska buddhistiska sekter tolkas detta som att det finns nivåer av upplysning bortom Buddhas nirvana. Nagarjuna själv betonade vikten av rätt leverne och goda handlingar.

andra bloggar om

filosofi, religion, buddhism, logik,